combining two statistical parameters to get best suitability

R square value (coefficient of determinant) and root mean square error (rmse). These are typical parameters which shows, how two arrays are dependent from each other.

R square value shows tedency and is very easy calculated in MS Excel using command "=correl(array1[Ax:Ax+n];array2[Bx:Bx+n])^2" and it is calculated by formula

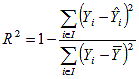
Root mean square error shows difference between two given data arrays. It is calculated by taking each data pair and getting their difference, and finally RMSE is equivalent to standart deviation of all these differences. Not too complicated as it seems.

R-squared is between 0 and 1. Usually RMSE is absolute and something positive (newertheless differences between data pairs still could be negative, but standart deviation always will be positive, even calculated from negative data - it is absolute deviation). But it is possible to get RMSE value relative, knowing each data array minimum and maximum values. Relative RMSE (RRMSE) = RMSE/maxx-minn

Now, both parameters are between 0 and 1.

Best suitability (BS) would be if R-squared = 1 (ascending) and RRMSE = 0 (descending)

BS = R^2-RMSE

Weights. Sometimes it is useful to give different weights to each of these statistical parameters. It`s simple - just multiply each coefficient with its weight.

I want that RMSE is twice hevier parameter than R^2.

BS = R^2 - RMSE*2

Sometimes it is useful to add some constante

BS = R^2 - RMSE + Const

but very rare.